개요
거품 정렬은 데이터를 '비교'하면서 찾기 때문에 '비교 정렬'이며 정렬의 대상이 되는 데이터 외에 추가적인 공간을 필요로 하지 않기 때문에 '제자리 정렬(in-place sort)'이기도 하다. 정확히는 데이터를 서로 교환하는 과정(swap)에서 임시 변수를 필요로 하나, 이는 충분히 무시할 만큼 적은 양이기 때문에 제자리 정렬로 보는 것이다. 이는 선택정렬과도 같은 부분이다.
그리고 이전에 다뤘던 선택 정렬과는 달리 거품 정렬은 앞에서부터 차례대로 비교하기 때문에 '안정 정렬'이기도 하다.
정렬 동작
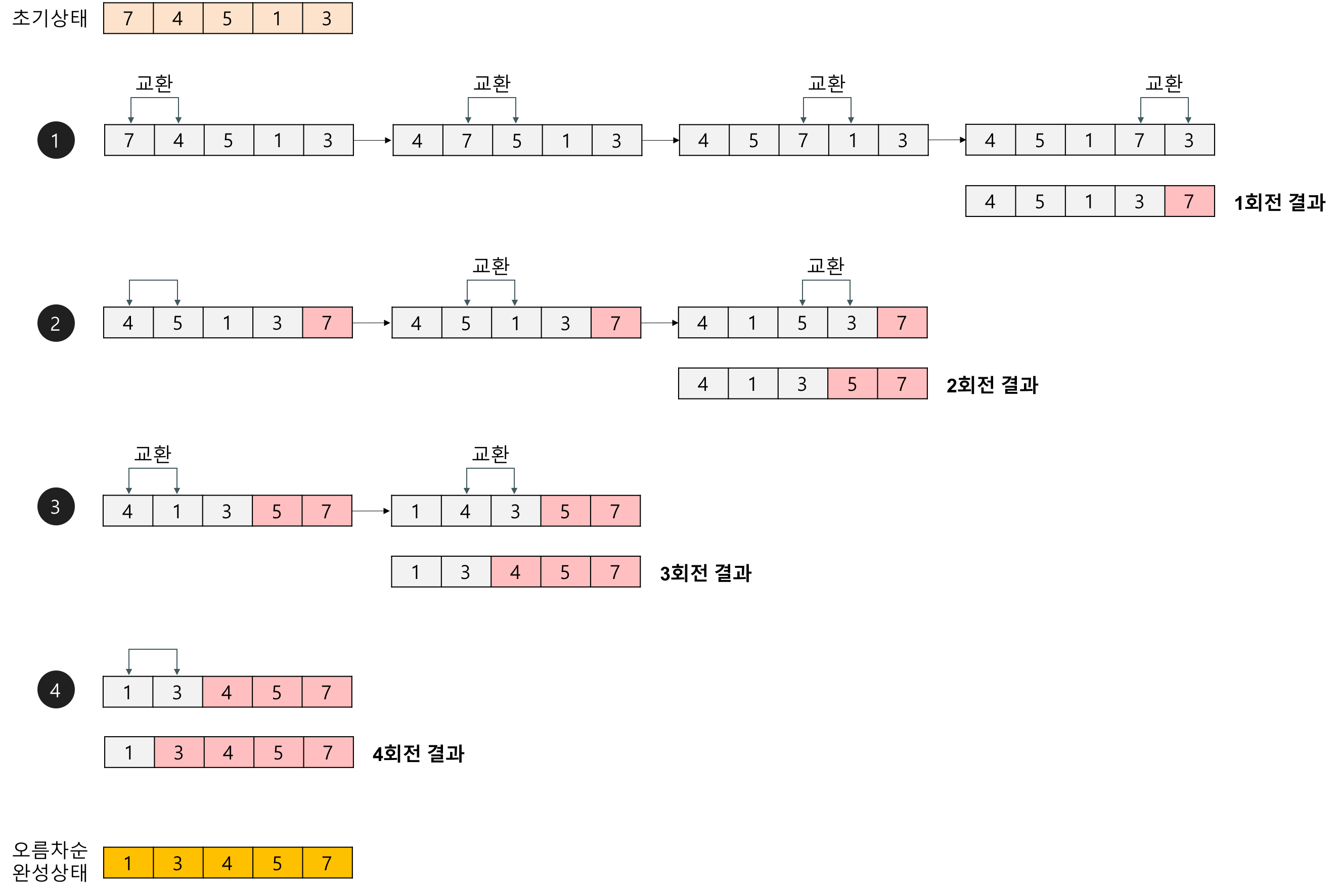
First Pass
- 첫 요소들을 시작으로 서로 인접한 두 요소를 순차적으로 비교한다.
- ( 5 1 4 2 8 ) –> ( 1 5 4 2 8 )
- ( 1 5 4 2 8 ) –> ( 1 4 5 2 8 )
- ( 1 4 5 2 8 ) –> ( 1 4 2 5 8 )
- ( 1 4 2 5 8 ) –> ( 1 4 2 5 8 )
Second Pass
- 정렬이 완료될 때까지 다음 이터레이션이 진행된다.
- 맨 끝 요소는 첫번째 이터레이션을 통해 가장 큰 요소임이 검증되었으므로 정렬에서 제외된다.
- 이터레이션이 돌면서 다음으로 검증된 최대값도 역시 그 다음 정렬에서 제외된다. (하나씩 정렬에서 제외)
- ( 1 4 2 5 8 ) –> ( 1 4 2 5 8 )
- ( 1 4 2 5 8 ) –> ( 1 2 4 5 8 )
- ( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )
- ( 1 2 4 5 8 ) –> ( 1 2 4 5 8 ) (8) swap 제외
Third Pass
- 두번째 이터레이션을 통해 정렬이 완료되었지만 알고리즘은 마지막으로 정렬이 완료되었는지 확인한다.
- *이 때 본 예제의 경우 두번의 이터레이션으로 정렬이 모두 완료되었음으로 모두 swap 하지 않는다.
- ( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )
- ( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )
- ( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )
- ( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )
구현 코드
기존 버블 정렬
class BubbleSort {
void bubbleSort(int arr[]){
int n = arr.length;
for (int i = 0; i < n - 1; i++)
for (int j = 0; j < n - i - 1; j++)
if (arr[j] > arr[j + 1]) {
// swap arr[j+1] and arr[j]
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
/* Prints the array */
void printArray(int arr[]){
int n = arr.length;
for (int i = 0; i < n; ++i)
System.out.print(arr[i] + " ");
System.out.println();
}
// Driver method to test above
public static void main(String args[]){
BubbleSort ob = new BubbleSort();
int arr[] = { 64, 34, 25, 12, 22, 11, 90 };
ob.bubbleSort(arr);
System.out.println("Sorted array");
ob.printArray(arr);
}
}
향상된 버블 정렬 구현
// An optimized version of Bubble Sort
import java.io.*;
class GFG{
static void bubbleSort(int arr[], int n){
int i, j, temp;
boolean swapped;
for (i = 0; i < n - 1; i++){
swapped = false;
for (j = 0; j < n - i - 1; j++){
if (arr[j] > arr[j + 1]){
// swap arr[j] and arr[j+1]
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
swapped = true;
}
}
// IF no two elements were
// swapped by inner loop, then break
if (swapped == false)
break;
}
}
// Function to print an array
static void printArray(int arr[], int size)
{
int i;
for (i = 0; i < size; i++)
System.out.print(arr[i] + " ");
System.out.println();
}
// Driver program
public static void main(String args[])
{
int arr[] = { 64, 34, 25, 12, 22, 11, 90 };
int n = arr.length;
bubbleSort(arr, n);
System.out.println("Sorted array: ");
printArray(arr, n);
}
}
// This code is contributed
// by Nikita Tiwari.
시간 복잡도
시간복잡도를 계산하면 (n-1) + (n-2) + (n-3) + .... + 2 + 1 => n(n-1)/2이므로, O(n^2) 이다.
또한 Bubble Sort는 정렬이 되어있든 안되어있든 2개의 원소를 비교하기 때문에 최선/평균/최악의 경우 모두 시간복잡도가 O(n^2) 으로 동일하다.
참고)
https://www.geeksforgeeks.org/bubble-sort/?ref=gcse
Bubble Sort - GeeksforGeeks
A Computer Science portal for geeks. It contains well written, well thought and well explained computer science and programming articles, quizzes and practice/competitive programming/company interview Questions.
www.geeksforgeeks.org
'Algorithm > 개념 정리' 카테고리의 다른 글
| Insertion Sort (0) | 2022.06.03 |
|---|---|
| Selection Sort(작성중) (0) | 2022.06.01 |
| Two Pointers, Sliding Window (0) | 2022.05.25 |

